Deriving the formula for the Homography Matrix

Recently at work I was researching ML approaches to image matching, specifically SuperGlue / MAST3R / ALIKED and some similar methods.

The interesting part in all this was to find out that SuperPoint / SuperGlue are trained on synthetic data, and then in a self-superviser manner, without needing some sort of smart labeling procedure.

Inevitably, both of these methods being trained in a supervised manner, they need a sufficiently big dataset of Ground-Truth points pairs between a large corpus of images. I looked at what kind of data ALIKE specifically is trained on, and saw that one of the datasets provides images of planes with annotated true Homograhy transformation between cameras.

Mention of the HPatches dataset in the ALIKE paper

Now, I’ve of course heard about homographies before — that’s the matrix that, for a given plane, describes how to match a point on one camera with a point on another camera if they’re observing the same point on that plane.

But after looking at this, and reviewing all my knowledge, I thought… why does a simple matrix work? Why is remapping a pixel from one camera to the other, given they’re looking at a plane, describable with a single matrix (in homogeneous coordinates)?

This was leaving me dumbfounded because I couldn’t simply come up with an intuitive explanation of why we couldn’t apply some kind of similar assumption to any other shape. If two cameras looked at a sphere instead of a plane, would the mapping of pixels from one camera to the other also be describable with a linear matrix? Of course not, the projection of rays from a camera to a sphere is a very non-linear operation, so why would the relation of matching pixels between two cameras be linear in this case?

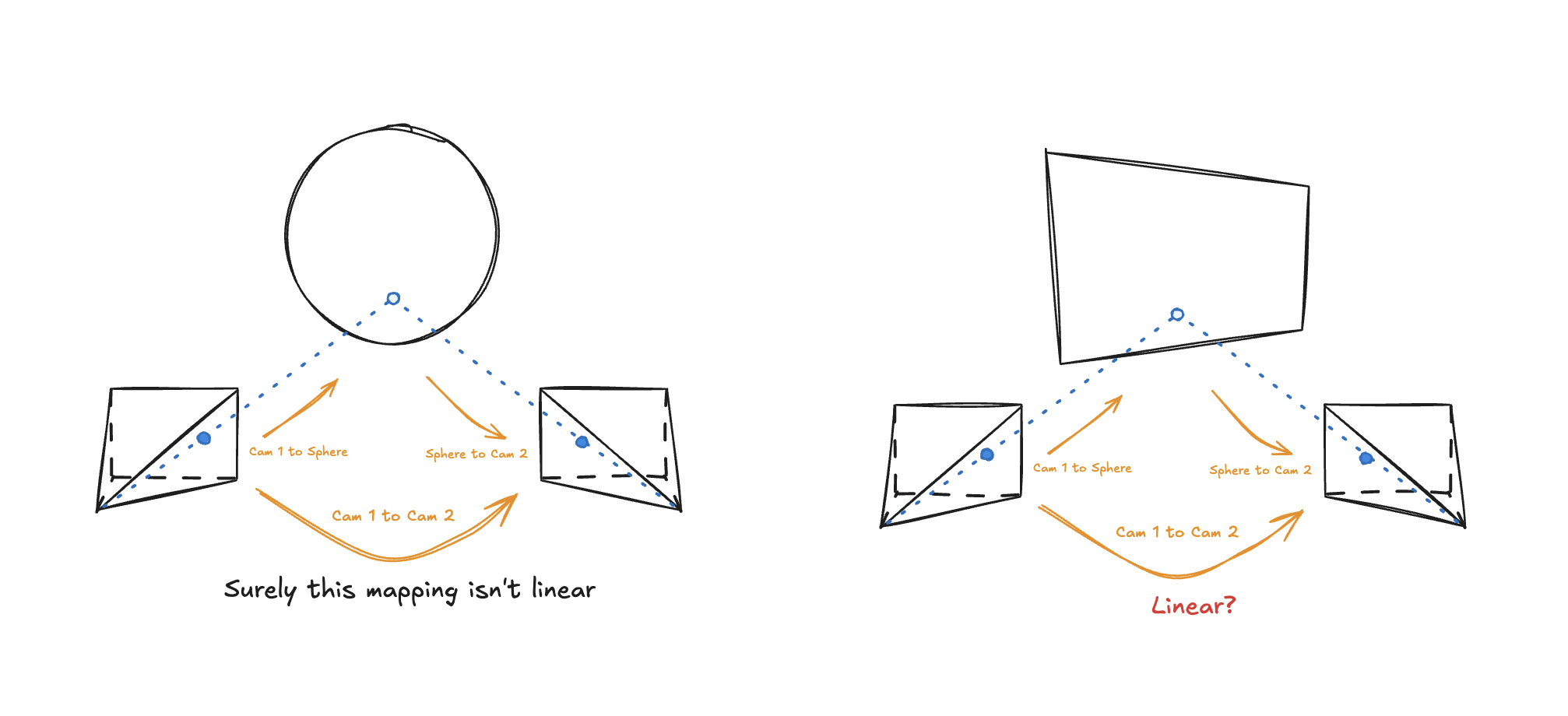Mapping between cameras, in the case of a sphere and a plate

Anyways, I started jumping through various online resources about what homographies really are but none really satisfied my need to understand the underlying logic.

Some resources did provide a sufficient proof for existence of a homography matrix and it being linear, but they did it through just proving the formula of deriving the homography matrix through 4 point correspondences between 2 cameras. And then just by the ability to express any other point on the plane as a linear combination of those 4 points, the matrix holds true for all points on the plane.

But that feels like cheating — I wanted to get a proof / formula irrespective of the particular points, just from the camera parameters / plane parameters alone.

So, here’s my pretty detailed derivation of the formula for the homography matrix, given just the camera/plane parameters:

Now this is what I’m talking about!

Going through this process did build a seed of intuition about homographic transformations in me, and why they’re linear (up to a scale, i.e. in homogeneous space!): if you parameterize the plane the way I did — it’s the most linear thing ever. I.e. the generator function for the plane points is linear (just take literally any 2D point, convert to a homogeneous point and multiply by a 3x3 matrix). All of this kinda leads to the idea that it probably is linear.